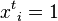Analysis of Taxi Drivers’ Behaviors Within a Battle Between Two Taxi Apps

This article revolves around a battle between two taxi giants in China, namely Didi and Kuaidad, who are backed by Internet giants Tencent and Alipay themselves. Taxi hiring is the latest thing to go online and is a booming topic for us data analysis enthusiast. We will try to look into what happened in 2014 which changed the Chinese Taxi hiring patterns for good. Data of around 9000 taxis was collected for 37 days and analysed. 

Taxi booking via mobile booking is the new and supposedly easy way of booking taxisaround the world. However what happened in China in 2014, made people study the affects and reasons on what are the possible advantages and drawbacks of this system.For starters, not everyone has a smartphone to book taxi, moreover these facilities are not available in the remotest part of a city. Mobile based taxi booking has its advantages as well. In retrospect of a passenger, who relies on taxi to travel, it can get very difficult to find a taxi in peak rush hours. When you get a taxi in just one click of your smartphone, you don't stand in scorching sun to wait for a taxi to see your waving hand and take you to desired destination. In driver's perspective this is a debatable issue. While some might argue that, it increases driver's efficiency, some may argue that it reduces driver's idel time and others argue that it makes a driver morally corrupt as he prefers to take smaller distance passenger and may bring unfairness to all the users. Next we see the Data analysis done and various  computations done to analyse the situation.

The data set used in this paper includes about 8.3 million taxi trips made by over 9000 taxis during 40 days.

The histogram plot of the numbers of trips made by every vehicle. In the first time period, the battle had not occurred) and in the second time period, the battle is white-hot.
We take a look at the  four taxi service indices: 
1) The distributions of the number of trips served by every vehicle per day during two periods, respectively.
2) The distributions of the idle time lengths of every vehicle before per trip during two periods, respectively.
3) The distributions of the traveling distances per trip during two periods, respectively.
4) The spatial distributions of the origins and destinations of passengers during two periods, respectively.

The graphs below show the recorded data:




The average numbers of passengers served per half hour during two time periods.






The empirical distributions of the idle time lengths of every vehicle before per tr-ip in each day of two time periods.











The empirical distributions of the traveling distance of every vehicle per trip in each day of two time periods.
It was observed that there was a significant change in hiring pattern for short distance trips whereas the pattern remained almost same for long distance trips, say more than 6km. This was because of the promotion money that was kicking in, which was dependent on number of trips made. These short-distance trips did not consume much time and were usually finished one by one so that their time gaps are small.





We further compare the numbers of taxis service happened at different locations with and without money promotion. We grid the central part of Beijing city into 1600 area grids. Each grid covers a 1 km × 1 km square. Above figure shows that the numbers of the incremental trips in 70% of these area grids are nearly zero. In other words, the taxis services are approximately the same under money promotion in such grids.

To conclude, this study was induced by the competition between internet giants who wanted to settle their business in mobile business industry. They started giving promotion money to taxi driver on completion of a taxi trip, which led to some hypothesis about drivers, which include foul practices on drivers side like prefering short distance trips, increased efficiency of drivers etc. Government was forced to shut down these mobile based taxi booking company in peak hours to provide equal treatment to all who seek taxis. 

This is all for this article, more to follow as I read follow up papers.

Resolution Limit in Community Detection

Modularity optimization seems to be a very effective method to detect communities, both in real and in artificially generated networks. However, modularity itself has not yet been thoroughly investigated, and only a few general properties are known.It is thus a priori impossible to tell whether a module (large or small), detected through modularity optimization, is indeed a single module or a cluster of smaller modules. This raises doubts about the effectiveness of modularity optimization in community detection, and more generally about the applicability of quality functions. 

The modularity of a partition of a network can be written as  

where the sum is over the m modules of the partition, l_s is the number of links inside module s, L is the total number of links in the network, and d_s is the total degree of the nodes in module s. The first term of the summand in equation is the fraction of links inside module s; the second term, in contrast, represents the expected fraction of links in that module, if links were located at random in the network (under the only constraint that the degree sequence coincides with the one of the original graph). If, for a subgraph S of a network, the first term is much larger than the second, it means that there are many more links inside S than one would expect by random chance. This means that S is, indeed, a module. The comparison with the null model (represented by the randomized network) leads to the quantitative definition of community embedded . We conclude that, in a modularity-based framework, a subgraph with l_s internal links and total degree d_s is a module if 

 

We can express the number of links l_s ^out joining nodes of the module s to the rest of the network in terms of l_s , i.e. l_s ^out = al_s with a ≥ 0. Therefore, d_s = 2l_s + l_s ^out = (a + 2)l_s and the condition become

from which, rearranging terms, one obtains 

If a = 0, the subgraph S is a disconnected part of the network and is a module if l_s < L, which is always true. If a is strictly positive, sets an upper limit to the number of internal links that S must have in order to be a module. This is counterintuitive, because it means that the definition of community implied by modularity depends on the size of the whole network, instead of involving a “local” comparison between the number of internal and external links of the module. For a < 2 one has 2l_s > l_s ^out, which means that the total internal degree of the subgraph is larger than its external degree: d_s ⁱⁿ > d_s ^out. The attributes “internal” and “external” mean that the degree is calculated considering only internal or external links, respectively. In this case, the subgraph S would be a community. For a < 2, the right-hand-side of inequality is in the interval [L/4, L]. A subgraph of size l_s such that a < 2 and l_s is less than a quantity in the interval [L/4, L] would then be a community both within the modularity framework . Sufficient conditions for which these constraints are always met are then.

 According to this equation, a partition of a network into actual modules (i.e. subgraphs satisfying the condition  ) would have a positive modularity, as all summands are positive. On the other hand, it is possible to partition a network such that Q is negative. The network itself, considered as a partition with a single module, has modularity zero: in this case, in fact, l ₁ = L, d ₁ = 2L, and the only two terms of the unique module in Q cancel each other. Usually, a value of Q larger than 0.3–0.4 is a clear indication that the subgraphs of the corresponding partition are modules. However, the maximal modularity differs from one network to another and depends on the number of links of the network. 

The fact that quality functions such as modularity can have an intrinsic resolution limit calls for a new theoretical framework that focuses on a local definition of community, rather than on definitions relying on a global null model. Quality functions are still helpful, but their role should probably be limited to the comparison of partitions with the same number of modules.

FURTHER READING : 

 http://www.pnas.org/content/104/1/36.full

Tracking Communities in Social Networks

Blogging is not rocket science it's about being yourself and putting what you have into it.. and when it's about Complex Networks then definitely I remember Albert Einstein's statement "Any fool can make things bigger, more complex and more violent. It takes a touch of genius and a lot of courage to move in the opposite direction.."

A social network is usually modeled as a graph in which vertices represent entities and edges represent interactions between pairs of entities.Previously,a community was often defined to be a subset of vertices that are densely connected internally but sparsely connected to the rest of the network. Accordingly, the best community of the graph was typically a peripheral set of vertices barely connected to the rest of the network by a small number of edges. However, as per the new view that for large-scale real-world societies, communities, though better connected internally than expected solely by chance, may also be well connected to the rest of the network.It is hard to imagine a small close-knit community with only a few edges connecting it to the outside world.

As shown the Computer Science community may be well attached to other parts of the network as well.  

With this intuitive notion of community, two types of structures are defined: the “whiskers” and the “core”. Whiskers are peripheral subsets of vertices that are barely connected to the rest of the network, while the core is the central piece that exclusively contains the type of community we are interested in. Then, the algorithm for finding a community can be reduced to two steps: 

•  identifying the core in which no whiskers exist
•  identifying communities in the core.

In this way, one can obtain communities that are not only more densely connected than expected by chance alone, but also well connected to the rest of the network. Much of the early work on finding communities in social networks focused on partitioning the corresponding graph into disjoint sub components. Algorithms often required dense graphs and conductance was widely taken as the measure of the quality of a community. Given a graph G = (V, E), the conductance of a subset of vertices S ⊆ V is defined as:

 where the  are the entries of the adjacency matrix for G and a(S) is the total number (or weight) of the edges incident with S. A subset was considered to be community-like when it had low conductance value. However, as discussed earlier, an individual may belong to multiple communities at the same time and will likely have more connections to individuals outside of his/her community than inside. One approach to finding such well-defined overlapping communities is the concept of an (α, β)-community and several algorithms were given for finding an (α, β)-community in a dense graph under certain conditions. Given a graph G = (V, E) with self-loops added to all vertices, a subset C ⊆ V is called an (α, β)-community when each vertex in C is connected to at least β vertices of C (self-loop counted) and each vertex outside of C is connected to at most α vertices of C (α < β).

Among the interesting questions being explored are why (α, β)-communities correspond to well-defined clusters and why there is no sequence of intermediate (α, β)- communities connecting one cluster to another. Other intriguing questions include whether different types of social networks incorporate fundamentally different social structures; what it is about the structure of real-world social networks that leads to the structure of cores, as in the Twitter graph, and why some synthetic networks do not display this structure. 

By taking the intersection of a group of massively overlapping (α, β)-communities obtained from repeated experiments, one can eliminate random factors and extract the underlying structure. In social graphs, for large community size k, the (α, β)- communities are well clustered into a small number of disjoint cores, and there are no isolated (α, β)-communities scattered between these densely-clustered cores. The number of cores decreases as k increases and becomes relatively small for large k. The cores obtained for a smaller k either disappear or merge into the cores obtained for a larger k. Moreover, the cores correspond to dense regions of the graph and there are no bridges of intermediate (α, β)-communities connecting one core to another. In contrast, the cores found in several random graph models usually have significant overlap among them, and the number of cores does not necessarily decrease as k increases. Extensive experiments demonstrate that the core structure displayed in various large-scale social graphs is, indeed, due to the underlying social structure of the networks, rather than due to high-degree vertices or to a particular degree distribution.

RESOLUTION LIMIT :  A popular method for community identification  now widely used relies on the optimization of a quantity called modularity, which is a quality index for a partition of a network into communities. If one chooses modularity as the relevant quality function, the problem of community detection becomes equivalent to modularity optimization. The latter is not trivial, as the number of possible partitions of a network into clusters increases at least exponentially with the size of the network, making exhaustive optimization computationally unfeasible even for relatively small graphs. Therefore, a number of algorithms have been devised to find a good optimization technique with the smallest computational cost possible. 

It is impossible to tell whether a module (large or small), detected through modularity optimization, is indeed a single module or a cluster of smaller modules. This raises doubts about the effectiveness of modularity optimization in community detection, and more generally about the applicability of quality functions.

So I guess it's time to wind up. Resolution Limit shall be covered in the next blog.Hope you all liked it.Waiting for your responses.

REFERENCES : 

• http://www.pnas.org/content/104/1/36.full
• http://www.jstor.org/stable/30035025?seq=1#page_scan_tab_contents This is an excellent paper on meeting strangers and friends of friends.
• http://www.cs.cornell.edu/~lwang/wang11ijsi.pdf

Percolation Centrality

A number of centrality measures to measure the importance of a node in the graph already exist like the Eigen vector centrality, Katz centrality, Closeness centrality, Betweenness centrality etc. All these centrality measures depend on the topology or structure of the graph and they do not change over time unless the structure of the graph changes. These centrality measure do not take into account the "state" of a node in the graph. That is to say, in networks with some kind of percolation like the spread of an infectious disease or the spread of a computer virus or the spread of a certain news in a social network etc, these measures would stay the same over time even though the percolation "states" of the nodes change. Here the "state" may represent whether the node is infected or not. Thus, a node may be central to a graph in terms of closeness centrality or some other measure but may not be central to the percolation network in the graph.

Percolation centrality is a centrality designed to capture this centrality measure in networks with percolation. The percolation centrality of a node at a given time is defined as the proportion of "percolated paths" that go through that node. Here, a percolated path is the shortest path between two nodes where the source node is in percolated state while the destination node may be percolated or non-percolated or partially percolated.

Here, PC is the percolation centrality of the node v.  is the total number of shortest paths present from node s to node r.  is the total number of shortest paths present from node s to node r that pass through node v.  is the percolation state of node i at time t.  represents node i is in non-percolated state while   represents node i being in fully percolated state.

The relative contribution (weight) of a percolated path from node s to node v is given by its weight as,

                                                        

Thus, the percolation state of the source node determines how much importance will the percolation path have in its contribution to the percolation centrality of node v. The summation term in the denominator is the total extent of percolation in the network ranging from 0 to N where N is the number of nodes in the network. For appropriate normalization of the weights, the percolation state of the node v is subtracted from the denominator. Thus,

Note that in the case of a fully percolated network, i.e  for all possible sources as well as the node v itself, the percolation centrality is equal to the betweenness centrality of the node. Since the percolation state of all the nodes are the same, all the percolated paths will the same weight i.e. the same contribution in the percolation centrality. As a result, in a fully percolated network, calculating the percolation centrality is the same as calculating the betweenness centrality. For a fully percolated network,

where BC is the betweenness centrality of the node v.

As shown in the figure, as the percolation becomes universal, the ratio of average PC and BC settles around unity, as PC converges to BC for every node.

Links for further reading:

1.Centrality measures

2. Percolation Centrality

Epidemic Dynamics in Complex Networks

Epidemic Dynamics in Complex Networks

Complex networks are currently being studied across many fields of science. Undoubtedly, many systems in nature can be described by models of complex networks, which are structures consisting of nodes or vertices connected by links or edges. Examples are numerous. The Internet is a network of routers or domains. The World Wide Web (WWW) is a network of websites. The brain is a network of neurons. An organization is a network of people.

Considering of the epidemic dynamics in Complex Networks, the AIDS propagation network is quite typical. When AIDS first emerged as a disease about twenty years ago, few people could have predicted how the epidemic would evolve, and even fewer could have been able to describe with certainty the best way of fighting it. Unfortunately, according to estimates from the Joint United Nations Programme on HIV/AIDS (UNAIDS) and the World Health Organization (WHO), 21.8 million people around the world had died of AIDS up to the end of 2000 and 36.1 million people were living with the human immunodeficiency virus (HIV) by the same time.

As another example, in spite of technological progress and great investments to ensure a secure supply of electric energy, blackouts of the electric transmission grid are not uncommon. Cascading failures in large-scale electric power transmission systems are an important cause of the catastrophic blackouts. Most well known is the cascading series of failures in power lines in August 1996, leading to blackouts in 11 US states and two Canadian provinces. This incident left about 7 million customers without power for up to 16 hours, and cost billions of dollars in total damage. There is an urgent need for developing innovative methodologies and conceptual breakthroughs for analysis, planning,operation, and protection of the complex and dynamical electric power networks. In yet another example, the ILOVEYOU computer virus spread over the Internet in May 2000 and caused a loss of nearly 7 billion dollars in facility damage and computer down-time.

How do diseases, jokes, and fashions spread out over the social networks? How do cascading failures propagate through large-scale power grids? How do computer viruses spread out through the Internet? Serious issues like these are attracting much attention these days. Clearly, the topology of a network has great influence on the overall behaviour of an epidemic spreading in the network.

Recently, some researchers have started to study such spreading phenomena, for example on small-world and scale-free networks. A notable attempt of Pastor-Satorras and Vespignani was to study both analytically and numerically a large-scale dynamical model on the spreading of epidemics in complex networks. The standard susceptible infected- susceptible (SIS) epidemiological model was used for investigation. 

Each node of the network represents an individual, and each link is a connection along which the infection can spread from one individual to some others. It is natural to assume that each individual can only exist in one of two discrete states—susceptible and infected. At every time step, each susceptible node is infected with probability υ if it is connected to at least one infected node. At the same time, infected nodes are cured and become again susceptible with probability δ. They together define an effective spreading rate, λ = υ/δ.

The updating can be performed with both parallel and sequential dynamics. The main prediction of the SIS model in homogeneous networks (including lattices, random graphs, and small-world models) is the presence of a non-zero epidemic threshold, λc > 0. If λ ≥ λc, the infection spreads and becomes persistent in time; yet if λ < λc, the infection dies out exponentially fast.(Fig 13(a))

It was found that, while for exponential networks the epidemic threshold is a positive constant, for a large class of scale-free networks the critical spreading rate tends to zero (Fig. 13(b)). In other words, scale-free networks are prone to the spreading and the persistence of infections, regardless of the spreading rate of the epidemic agents. It implies that computer viruses can spread far and wide on the Internet by infecting only a tiny fraction of the huge network. Fortunately, this is balanced by exponentially small prevalence and by the fact that it is true only for a range of very small spreading rates (λ << 1) that tend to zero.

Closeness centrality in networks with disconnected components

Closeness centrality in networks with disconnected components

A key node centrality measure in networks is closeness centrality (Freeman, 1978; Opsahl et al., 2010; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.

This network gives a concrete example of the closeness measure. The distance between node G and node H is infinite as a direct or indirect path does not exist between them (i.e., they belong to separate components). As long as at least one node is unreachable by the others, the sum of distances to all other nodes is infinite. As a consequence, researchers have limited the closeness measure to the largest component of nodes (i.e., measured intra-component). The distance matrix for the nodes in the sample network is:

	Nodes												All inclusive		Intra-component
	A	B	C	D	E	F	G	H	I	J	K		Farness	Closeness	Farness	Closeness
A	…	1	1	2	2	3	3	Inf	Inf	Inf	Inf		Inf	0	12	0.08
B	1	…	1	2	1	2	3	Inf	Inf	Inf	Inf		Inf	0	10	0.10
C	1	1	…	1	2	2	2	Inf	Inf	Inf	Inf		Inf	0	9	0.11
D	2	2	1	…	2	1	1	Inf	Inf	Inf	Inf		Inf	0	9	0.11
E	2	1	2	2	…	1	3	Inf	Inf	Inf	Inf		Inf	0	11	0.09
F	3	2	2	1	1	…	2	Inf	Inf	Inf	Inf		Inf	0	11	0.09
G	3	3	2	1	3	2	…	Inf	Inf	Inf	Inf		Inf	0	14	0.07
H	Inf	Inf	Inf	Inf	Inf	Inf	Inf	…	1	2	Inf		Inf	0	3	0.33
I	Inf	Inf	Inf	Inf	Inf	Inf	Inf	1	…	1	Inf		Inf	0	2	0.50
J	Inf	Inf	Inf	Inf	Inf	Inf	Inf	2	1	…	Inf		Inf	0	3	0.33
K	Inf	Inf	Inf	Inf	Inf	Inf	Inf	Inf	Inf	Inf	…		Inf	0	0	Inf

Although the intra-component closeness scores are not infinite for all the nodes in the network, it would be inaccurate to use them as a closeness measure. This is due to the fact that the sum of distances would contain different number of paths (e.g., there are two distance from node H to other nodes in its component, while there are six distances from node G to other nodes in its component). In fact, nodes in smaller components would generally be seen as being closer to others than nodes in larger components. Thus, researchers has focused solely on the largest component. However, this leads to a number of methodological issues, including sample selection.

To develop this measure, I went back to the original equation:

where  is the focal node,  is another node in the network, and  is the shortest distance between these two nodes. In this equation, the distances are inversed after they have been summed, and when summing an infinite number, the outcome is infinite. To overcome this issue while staying consistent with the existing measure of closeness, I took advantage of the fact that the limit of a number divided by infinity is zero. Although infinity is not an exact number, the inverse of a very high number is very close to 0. In fact, 0 is returned if you enter 1/Inf in the statistical programme R. By taking advantage of this feature, it is possible to rewrite the closeness equation as the sum of inversed distances to all other nodes instead of the inversed of the sum of distances to all other nodes. The equation would then be:

To exemplify this change, for the example network above, the inversed distances and closeness scores are:

	Nodes												Closeness
	A	B	C	D	E	F	G	H	I	J	K		Sum	Normalized
A	…	1.00	1.00	0.50	0.50	0.33	0.33	0	0	0	0		3.67	0.37
B	1.00	…	1.00	0.50	1.00	0.50	0.33	0	0	0	0		4.33	0.43
C	1.00	1.00	…	1.00	0.50	0.50	0.50	0	0	0	0		4.50	0.45
D	0.50	0.50	1.00	…	0.50	1.00	1.00	0	0	0	0		4.50	0.45
E	0.50	1.00	0.50	0.50	…	1.00	0.33	0	0	0	0		3.83	0.38
F	0.33	0.50	0.50	1.00	1.00	…	0.50	0	0	0	0		3.83	0.38
G	0.33	0.33	0.50	1.00	0.33	0.50	…	0	0	0	0		3.00	0.30
H	0	0	0	0	0	0	0	…	1.00	0.50	0		1.50	0.15
I	0	0	0	0	0	0	0	1.00	…	1.00	0		2	0.20
J	0	0	0	0	0	0	0	0.50	1.00	…	0		1.50	0.15
K	0	0	0	0	0	0	0	0	0	0	…		0	0

As can be seen from this table, a closeness score is attained for all nodes taking into consideration an equal number of distances for each node irrespective of the size of the nodes’ component. Moreover, nodes belonging to a larger component generally attains a higher score. This is deliberate as these nodes can reach a greater number of others than nodes in smaller components. The normalized scores are bound between 0 and 1. It is 0 if a node is an isolate, and 1 if a node is directly connected all others.

This measure can easily be extended to weighted networks by introducing Dijkstra’s (1959) algorithm.

What to try it with your data?

Below is the code to calculate the closeness measure on the sample network above.

1 2 3 4 5 6 7 8 9 10 11 12

# Load tnet library(tnet) # Load network # Node K is assigned node id 8 instead of 10 as isolates at the end of id sequences are not recorded in edgelists net <- cbind(   i=c(1,1,2,2,2,3,3,3,4,4,4,5,5,6,6,7,9,10,10,11),   j=c(2,3,1,3,5,1,2,4,3,6,7,2,6,4,5,4,10,9,11,10),   w=c(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)) # Calculate measures closeness_w(net, gconly=FALSE)