Percolation Centrality
A number of centrality measures to measure the importance of a node in the graph already exist like the Eigen vector centrality, Katz centrality, Closeness centrality, Betweenness centrality etc. All these centrality measures depend on the topology or structure of the graph and they do not change over time unless the structure of the graph changes. These centrality measure do not take into account the "state" of a node in the graph. That is to say, in networks with some kind of percolation like the spread of an infectious disease or the spread of a computer virus or the spread of a certain news in a social network etc, these measures would stay the same over time even though the percolation "states" of the nodes change. Here the "state" may represent whether the node is infected or not. Thus, a node may be central to a graph in terms of closeness centrality or some other measure but may not be central to the percolation network in the graph.
Percolation centrality is a centrality designed to capture this centrality measure in networks with percolation. The percolation centrality of a node at a given time is defined as the proportion of "percolated paths" that go through that node. Here, a percolated path is the shortest path between two nodes where the source node is in percolated state while the destination node may be percolated or non-percolated or partially percolated.
Percolation centrality is a centrality designed to capture this centrality measure in networks with percolation. The percolation centrality of a node at a given time is defined as the proportion of "percolated paths" that go through that node. Here, a percolated path is the shortest path between two nodes where the source node is in percolated state while the destination node may be percolated or non-percolated or partially percolated.
![PC^t(v)= \frac{1}{N-2}\sum_{s \neq v \neq r}\frac{\sigma_{sr}(v)}{\sigma_{sr}}\frac{{x^t}_s}{{\sum {[{x^t}_i}]}-{x^t}_v}](https://upload.wikimedia.org/math/2/c/5/2c5a141857c7e0a873385e613ab57d1b.png)
Here, PC is the percolation centrality of the node v. 
is the total number of shortest paths present from node s to node r. 
is the total number of shortest paths present from node s to node r that pass through node v. 
is the percolation state of node i at time t. 
represents node i is in non-percolated state while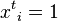 
represents node i being in fully percolated state.
is the total number of shortest paths present from node s to node r. is the total number of shortest paths present from node s to node r that pass through node v. is the percolation state of node i at time t. represents node i is in non-percolated state while 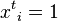represents node i being in fully percolated state.
The relative contribution (weight) of a percolated path from node s to node v is given by its weight as,
Thus, the percolation state of the source node determines how much importance will the percolation path have in its contribution to the percolation centrality of node v. The summation term in the denominator is the total extent of percolation in the network ranging from 0 to N where N is the number of nodes in the network. For appropriate normalization of the weights, the percolation state of the node v is subtracted from the denominator. Thus,
Note that in the case of a fully percolated network, i.e 
for all possible sources as well as the node v itself, the percolation centrality is equal to the betweenness centrality of the node. Since the percolation state of all the nodes are the same, all the percolated paths will the same weight i.e. the same contribution in the percolation centrality. As a result, in a fully percolated network, calculating the percolation centrality is the same as calculating the betweenness centrality. For a fully percolated network,
for all possible sources as well as the node v itself, the percolation centrality is equal to the betweenness centrality of the node. Since the percolation state of all the nodes are the same, all the percolated paths will the same weight i.e. the same contribution in the percolation centrality. As a result, in a fully percolated network, calculating the percolation centrality is the same as calculating the betweenness centrality. For a fully percolated network,
where BC is the betweenness centrality of the node v.
As shown in the figure, as the percolation becomes universal, the ratio of average PC and BC settles around unity, as PC converges to BC for every node.
Links for further reading:
No comments:
Post a Comment