Influencers For Destruction

Structural Influencers

The problem of finding an optimal set of structural nodes which if immunized, would prevent the diffusion of a large scale of epidemic or if destroyed would lead to the structural collapse of a network is well known in the literature of complex networks with various potential applications in cybersecurity and disease control. For example one can eliminate a bacteria by selectively disrupting their molecular network or contain a epidemic spread my vaccinating few selected individuals in a population and breaking the connection network of the pathogen. This minimal set of structural nodes are called, influencers and localizing them is one of the most important problems in network science. This problem of identifying the optimal set of nodes for which deletion would cause maximum damage is a NP-hard problem which means it becomes prohibitively expensive for large networks.

Influencers and Percolation

Flaviano Morone and Hernan A. Makse recently developed an approximate and scalable algorithm for finding minimal set of such nodes which when removed dismantles the giant component of the network into multiple much smaller clusters. The trick they used is to map this problem of optimal influencers onto optimal percolation of a tree like random networks. Percolation is related to the connectedness of a network. Given a random graph of n nodes and an average degree  . If we remove randomly a fraction 1−p  of nodes and leave only a fraction p. There exists a critical percolation threshold   below which the network becomes fragmented while above p_c a giant connected component exists. From this mapping they derive an energy function with a minimum that corresponds to the set of nodes that need to eliminated to yield a network whose largest cluster is as small as possible. So finding this optimal influencers problem translates to finding the minimum fraction of influencers such that removing them vanishes the probability of existence of the giant component.

 

Collective Influence

To find this minima, Morone and Makse introduced the concept of collective influence, which is the product of the node's reduced degree (degree minus one) and the sum of the reduced degrees of the nodes that are at a certain steps away from it. This measure describes the number of nodes reachable from a given node assuming nodes of high collective influence have a crucial role in the network.

The basic idea here is to remove nodes causing the biggest drop in the energy function. First they define a ball of radius l around every every node and then consider the nodes belonging to the frontier and assign  to node i the collective influence (CI) strength at the level l using the above equation. This collective influence based algorithm then sequentially removes nodes, starting with nodes that have the highest collective influence and recalculating the collective influence of the rest following each operation. The authors have shown that this way of removing the nodes based on collective influence is more effective in fragmenting a network than other heuristic centrality measures like: high-degree (HD), high-degree adaptive (HDA), PageRank (PR), closeness centrality (CC), eigenvector centrality(EC) and k-core. The set of influencers identified surprisingly contains many nodes with few connections which highlights the fact that the importance of a node in ensuring a network's integrity is determined not only by the number of direct links, but also by which other nodes it's connected to. The collective influence measure for l >= 1 has a rich topological content and tells much more about the role played by the nodes. Hence even nodes with moderate or low degree surrounded by coronas of hubs have higher collective influence compared to the hubs themselves.

 

 Computational Complexity

Collective Influence algorithm is remarkably fast requiring only 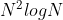computations to dismantle a network that contains N nodes. Its complexity is further reduced to 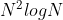if, instead of individual nodes, a fixed fraction of the total nodes is removed at each step of the computation. On the basis of spin-glass theory authors conclude that collective influence is expected to have small overlap with the optimal solution. Hence it should be used with caution. However nodes selected by CI are more effective in destroying a network of nodes selected by other methods. So even though CI is an approximate method, it's faster and more efficient.

 

Future Work

CI has only one free parameter - the distance, expressed as number of steps from any given node. Although the authors find that distances greater than one works, a firm criterion for choosing an optimal value is lacking and would be next step. Also authors designed their algorithm to work on networks which are locally tree-like, further work is needed to validate it's accuracy on networks with loops. Also extending this work to link level operations instead of node level operations can extend it's applicability to areas where node level interventions are too drastic.

Finally this work on identification of optimal influencers can be used towards building networks that would be robust against both attacks and failures in areas with profound implications like cybersecurity, fault-tolerant power grids and development of drugs etc.

References:

1. Flaviano Morone & Hernan A. Makse, Influence maximization in complex networks through optimal percolation.

2. Istvan A. Kovacs & Albert-Laszlo Barabasi, Destruction Perfected

3. Percolation theory, Wikipedia

4. Random Graph, Wikipedia